Numerical quantum dynamics using WavePacket: I. Closed quantum systems and discrete variable representations: Difference between revisions
mNo edit summary |
|||
| (15 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
* Publication also listed at [https://zbmath.org/?q=an%3A1376.81005 zbMATH:1376.81005] | * Publication also listed at [https://zbmath.org/?q=an%3A1376.81005 zbMATH:1376.81005] | ||
* Software also listed at [https://zbmath.org/software/19829 swMATH:19829] | * Software also listed at [https://zbmath.org/software/19829 swMATH:19829] | ||
[[File:WavePacket logo.jpg|thumb|200x200px|WavePacket logo]] | |||
== Problem Statement == | == Problem Statement == | ||
| Line 14: | Line 15: | ||
=== Procedure === | === Procedure === | ||
[[File:WavePacket flowchart.jpg|alt=WavePacket flowchart|none|thumb|600x600px|WavePacket flowchart]] | |||
* '''qm_setup''': Before WavePacket simulations, initialize a wave function object. | * '''qm_setup''': Before WavePacket simulations, initialize a wave function object. | ||
| Line 28: | Line 28: | ||
* Femto-chemistry, see, e.g., 1996 nobel prize in chemistry for A.H.Zewail, [https://www.wikidata.org/wiki/Q106624 wikidata:Q106624] | * Femto-chemistry, see, e.g., 1996 nobel prize in chemistry for A.H.Zewail, [https://www.wikidata.org/wiki/Q106624 wikidata:Q106624] | ||
* Molecular physics, [https://www.wikidata.org/wiki/Q489328 wikipedia:Q489328] | * Molecular physics, [https://www.wikidata.org/wiki/Q489328 wikipedia:Q489328] | ||
=== Data Streams === | === Data Streams === | ||
| Line 37: | Line 35: | ||
== Model == | == Model == | ||
Isolated molecules (e.g. single molecules in electric, magnetic, optical traps, or in dilute gases), can be modeled as closed quantum systems. Their bound states <math>\Psi_n</math>, along with the energies <math>E_n</math>, are obtained as solutions of the '''TISE''' | Isolated molecules (e.g. single molecules in electric, magnetic, optical traps, or in dilute gases), can be modeled as closed quantum systems. Their bound states <math>\Psi_n(R)</math>, along with the energies <math>E_n</math>, are obtained as solutions of the '''TISE''' | ||
<math> \hat{H}(R,-i\nabla_R,t) \Psi_n = E_n \Psi_n </math> | <math> \hat{H}(R,-i\nabla_R,t) \Psi_n(R) = E_n \Psi_n(R) </math> | ||
Their dynamics is obtained as solution <math>\Psi(t)</math> of the '''TDSE''' ([https://www.wikidata.org/wiki/Q165498 wikidata:Q165498]) | Their dynamics is obtained as solution <math>\Psi(R,t)</math> of the '''TDSE''' ([https://www.wikidata.org/wiki/Q165498 wikidata:Q165498]) | ||
<math>\mathrm{i} \frac{\partial}{\partial t}\Psi(t) = \hat{H}(R,-i\nabla_R,t) \Psi(t) </math> | <math>\mathrm{i} \frac{\partial}{\partial t}\Psi(R,t) = \hat{H}(R,-i\nabla_R,t) \Psi(R,t) </math> | ||
=== Discretization === | === Discretization === | ||
| Line 88: | Line 86: | ||
===Parameters=== | ===Parameters=== | ||
Definition of WavePacket's standard Hamiltonian. If applicable, interaction with external electric fields is treated within the semi-classical dipole approximation (TDSE only). | Definition of WavePacket's standard Hamiltonian. If applicable, interaction with external electric fields <math>F(t)</math> through dipole moments <math>\mu(R)</math> and/or polarizabilities <math>\alpha(R)</math> is treated within the semi-classical dipole approximation (TDSE only). | ||
<math>H=T(R,-i\nabla_R)1+V(R)-iW(R)1-F(t)\cdot\mu(R)-\frac{1}{2}F^2(t)\cdot\alpha(R)</math> | <math>H=T(R,-i\nabla_R)1+V(R)-iW(R)1-F(t)\cdot\mu(R)-\frac{1}{2}F^2(t)\cdot\alpha(R)</math> | ||
| Line 197: | Line 195: | ||
|[[wikidata:Q52069558]] | |[[wikidata:Q52069558]] | ||
|Fourier grid Hamiltonian | |Fourier grid Hamiltonian | ||
| | |qm_bound | ||
|<math>n_\mathrm{max}</math> | |<math>n_\mathrm{max}</math> | ||
| WavePacket Software | | WavePacket Software | ||
|} | |} | ||
====Solving the TDSE==== | ====Solving the TDSE==== | ||
{| class="wikitable" | {| class="wikitable" | ||
| Line 211: | Line 210: | ||
|[[wikidata:Q2311789]] | |[[wikidata:Q2311789]] | ||
|Split-step method | |Split-step method | ||
| | |qm_propa | ||
|Time step <math>\Delta t</math> | |Time step <math>\Delta t</math> | ||
|WavePacket Software | |WavePacket Software | ||
| Line 217: | Line 216: | ||
|[[wikidata:Q115616698]] | |[[wikidata:Q115616698]] | ||
|Chebychev method | |Chebychev method | ||
| | | qm_propa | ||
|Time step <math>\Delta t</math> | |Time step <math>\Delta t</math> | ||
|WavePacket Software | |WavePacket Software | ||
| Line 223: | Line 222: | ||
|[[wikidata:Q115616932]] | |[[wikidata:Q115616932]] | ||
|Second order differencing | |Second order differencing | ||
| | |qm_propa | ||
|Time step <math>\Delta t</math> | |Time step <math>\Delta t</math> | ||
|WavePacket Software | |WavePacket Software | ||
| Line 256: | Line 255: | ||
|0.3.4 | |0.3.4 | ||
|C++/Python | |C++/Python | ||
| | |[https://github.com/juanjosegarciaripoll/tensor Tensor], [https://boost.org Boost.Numeric.Odeint], pybind11, numpy, matplotlib | ||
|git | |git | ||
|no | |no | ||
|Wiki | |Wiki | ||
|} | |}Extensive documentation is also available from this scientific article: | ||
*Comp. Phys. Comm. (2017), [https://doi.org/10.1016/j.cpc.2016.12.007 doi:10.1016/j.cpc.2016.12.007] | *Comp. Phys. Comm. (2017), [https://doi.org/10.1016/j.cpc.2016.12.007 doi:10.1016/j.cpc.2016.12.007] | ||
| Line 298: | Line 297: | ||
| - | | - | ||
|qm_init.m | |qm_init.m | ||
|tiny | |tiny [kB] | ||
|Matlab script | |Matlab script | ||
| - | |||
|m-file | |m-file | ||
| text | | text | ||
|yes | |yes | ||
| Line 322: | Line 321: | ||
|- | |- | ||
| - | | - | ||
|Log | |Log output, e.g. qm_propa.out | ||
|tiny [kB] | |tiny [kB] | ||
| - | |||
| - | | - | ||
| txt-file | | txt-file | ||
| text | | text | ||
|no | |no | ||
| Line 333: | Line 332: | ||
|- | |- | ||
| - | | - | ||
| | |Wave functions: <math>\Psi_n,\Psi(t)</math> | ||
|large [GB] | |large [GB] | ||
| - | | - | ||
| - | | - | ||
| mat-file | |||
|binary | |binary | ||
|yes | |yes | ||
| Line 344: | Line 343: | ||
|- | |- | ||
| - | | - | ||
| | | Snapshots | ||
|small [MB] | |||
| - | |||
| - | |||
| fig | |||
|binary | |||
|yes | |||
|yes | |||
|yes | |||
|- | |||
| - | |||
| Snapshots | |||
|small [MB] | |small [MB] | ||
| - | | - | ||
| - | | - | ||
| jpg | |||
|binary | |binary | ||
|no | |no | ||
| Line 358: | Line 368: | ||
|small [MB] | |small [MB] | ||
| - | | - | ||
| - | | - | ||
| mp4 | |||
|binary | |binary | ||
|no | |no | ||
Latest revision as of 14:19, 19 December 2022
- Author: Burkhard Schmidt, ORCID:0000-0002-9658-499X, personal web page: www.qcmd.info
- Publication also listed at zbMATH:1376.81005
- Software also listed at swMATH:19829

Problem Statement
Numerical quantum dynamics, wikidata:Q7269042
For atoms, molecules and possible also other fields, including interaction of quantum systems with external fields within the semi-classical dipole approximation
Object of Research and Objective
Although WavePacket is made for general quantum systems, so far it has been developed/used mainly for describing the dynamics of molecules, i.e., typically the motion of the comprising nuclei. Especially when low masses (e.g. hydrogen atoms), low energies, and/or low temperatures are involved, the dynamics of the nuclei may be subject to quantum effects. Hence, the modeling of small molecules should be based on quantum mechanical modeling. Because of the computational effort increasing steeply (exponentially?) with the number of atoms, this can not be done for large molecules. However, due to recent advances both in computer hardware and in modeling/algorithms, the border between small and large is constantly shifting toward the latter ...
Procedure
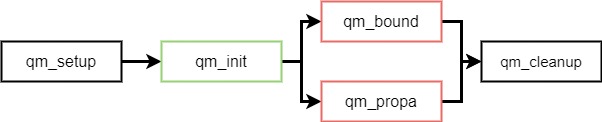
- qm_setup: Before WavePacket simulations, initialize a wave function object.
- qm_init: Initialize your simulation scenario, i.e. potential and kinetic energy operators, spatial and temporal discretization, coupling to external fields, set initial state.
- qm_bound: Solving the time-independent Schrödinger equation (TISE), i.e., calculate stationary bound states of a quantum system. Note that there is a substantial choice of spatial discretizations built-in for numerical solution of the TISE.
- qm_propa: Solving the time-dependent Schrödinger equation (TDSE), i.e., propagate the state of a quantum state in time. Note that there is a substantial choice of different integration methods built-in for numerical solution of the TDSE.
- qm_cleanup: After WavePacket simulations, clean up everything ...
Involved Disciplines
- Theoretical Chemistry, wikidata:Q321150
- Femto-chemistry, see, e.g., 1996 nobel prize in chemistry for A.H.Zewail, wikidata:Q106624
- Molecular physics, wikipedia:Q489328
Data Streams
Not sure what to write here. In some of the other workflows, data streams from and to projects in other consortia are mentioned here
Model
Isolated molecules (e.g. single molecules in electric, magnetic, optical traps, or in dilute gases), can be modeled as closed quantum systems. Their bound states , along with the energies , are obtained as solutions of the TISE
Their dynamics is obtained as solution of the TDSE (wikidata:Q165498)
Discretization
- Time (TDSE only): Equally spaced time steps; typically to be chosen inversely proportional to the spectrum of the spatially discretized Hamiltonian.
- Space: For each degree of freedom there is a choice of the following pseudo-spectral discretizations
- FFT methods, with equally spaced grid points: Mainly for molecular scattering, dissociation, association
- Gauss-Hermite: Mainly for molecular vibrations
- Gauss-Legendre: Mainly for molecular rotations
Due to the object-oriented concept and the open architecture, it is straightforward to add new classes for spatial discretizations.
Variables
Using atomic units (wikidata:Q757568) throughout WavePacket software
| Name | Symbol | Unit |
|---|---|---|
| number of bound states | n.a. | |
| initial time | a. t. u. | |
| final time | a. t. u. | |
| size of main time steps | a. t. u. | |
| number of sub steps | n.a. | |
| initial state | n.a. |
Parameters
Definition of WavePacket's standard Hamiltonian. If applicable, interaction with external electric fields through dipole moments and/or polarizabilities is treated within the semi-classical dipole approximation (TDSE only).
| Name | Symbol | Unit |
|---|---|---|
| spatial discretization | Bohr | |
| kinetic energy | Hartree | |
| potential energy | Hartree | |
| absorbing potential | Hartree | |
| electric field | a. u. | |
| dipole moment | a. u. | |
| polarizability | a. u. |
Process Informationen
Process Steps
Essentially the same as above, thus doubling information given in section "Procedure" ?!?
| Name | Description | Input | Output | Method | Parameter | Environment | Mathematical Area |
|---|---|---|---|---|---|---|---|
| qm_setup | Setup before simulations | --- | WavePacket object | --- | --- | Matlab | --- |
| qm_init | Initialize specific simulation | Set all input and parameters | Initial state | --- | --- | Matlab | --- |
| qm_bound | Stationary wave functions | Choose number of bound states | Bound states , energies | Solving the TISE, see below | All of the above parameters | Matlab | Numerical Mathematics |
| qm_propa | Propagate wave functions | Choose numerical propagator | Intermediate and final states | Solving the TDSE, see below | All of the above parameters | Matlab | Numerical Mathematics |
| qm_cleanup | Purge after simulations | --- | --- | --- | --- | Matlab | --- |
Applied Methods
The WavePacket software packages encompasses several different methods for numerical propagation of quantum states in time. Due to the object-oriented concept and the open architecture, it is straightforward to add new classes for the implementation of further numerical schemes. The aim could/should be to evolve WavePacket into a "laboratory" for numerical quantum dynamics.
Solving the TISE
| ID | Name | Process Step | Parameter | implemented by |
|---|---|---|---|---|
| wikidata:Q52069558 | Fourier grid Hamiltonian | qm_bound | WavePacket Software |
Solving the TDSE
| ID | Name | Process Step | Parameter | implemented by |
|---|---|---|---|---|
| wikidata:Q2311789 | Split-step method | qm_propa | Time step | WavePacket Software |
| wikidata:Q115616698 | Chebychev method | qm_propa | Time step | WavePacket Software |
| wikidata:Q115616932 | Second order differencing | qm_propa | Time step | WavePacket Software |
Note: WikiData entries for the latter two numerical methods were created by me (B. S.)
Software used
Software package: WavePacket project at SourceForge. This document is mainly on the mature and stable Matlab/Octave version of WavePacket. Note that there is also a C++/Python version which is still in an experimental phase (but making good progress recently). Both versions come with extended Wiki pages hosted along with the respective Sourceforge repositories.
| ID | Name | Description | Version | Programming Language | Dependencies | versioned | published | documented |
|---|---|---|---|---|---|---|---|---|
| SF.net | WavePacket | Numerical quantum dynamics | 7.0.0 | Matlab/Octave | n.a. | git, svn | see below | Wiki |
| SF.net | WavePacket | Numerical quantum dynamics | 0.3.4 | C++/Python | Tensor, Boost.Numeric.Odeint, pybind11, numpy, matplotlib | git | no | Wiki |
Extensive documentation is also available from this scientific article:
- Comp. Phys. Comm. (2017), doi:10.1016/j.cpc.2016.12.007
Hardware
WavePacket should run on any hardware for which Matlab (and a licence) is available
| ID | Name | Processor | Compiler | #Nodes | #Cores |
|---|---|---|---|---|---|
Input Data
All the input needed for a WavePacket simulation is encoded in a Matlab script called qm_init.m which has to be provided by the user. A large number of existing demo examples are expected to be very helpful for unexperienced users. Essentially, the input data therein match everything given above, see sections on "Variables" and "Parameters".
| ID | Name | Size | Data Structure | Format Representation | Format Exchange | binary/text | proprietary | to publish | to archive |
|---|---|---|---|---|---|---|---|---|---|
| - | qm_init.m | tiny [kB] | Matlab script | - | m-file | text | yes | yes | yes |
Output Data
Reproducibility
Mathematical Reproducibility
WavePacket reproduces several known analytic solutions of Schrödinger equations, see the demo examples on our Wiki pages. Among them well-known cases such as the quantum harmonic oscillator and the Morse oscillator, but also less widespread ones such as the generalized pendulum which is an intriguing example for conditionally quasi-exactly solvability (CQES), see wikidata:Q25111852 and our 2017 work, wikidata:Q59528631.
Runtime Reproducibility
Not sure what to write here
Reproducibility of Results
Not sure what to write here
Reproducibility on original Hardware
Originally developed on Windows-PCs. No changes of the results upon migrating from Win7 to Win10 and Win11. (No surprise because it is Matlab!)
Reproducibility on other Hardware
Reproducibility is ensured for Linux and iOS. (No surprise because it is Matlab!)
a) Serial Computation
b) Parallel Computation
So far, no specific efforts were taken to make WavePacket suitable for parallel computation. However, at least on multi-core-CPUs Matlab automatically uses several cores, e.g., when doing Fourier transforms or standard Linear Algebra tasks.
Transferability to
a) similar model parameters (other initial and boundary values):
The WavePacket program package comes with a choice of different model functions for
- Kinetic energy operators
- Potential energy functions
- Negative imaginary potentials
- Pulse shapes for electric fields
- (Permanent or transition) dipole moments
- Polarizability tensor
- Initial quantum states
If none of the provided model functions fits, the user has the choice either to write new ones or to provide tabulated data (→interpolation)
b) other models: Simulations of classical and quantum-classical dynamics also available within WavePacket using the same input, thus simulating exactly the same physical system. (This is a unique selling point)
Legend
The following abbreviations are used in the document to indicate/resolve IDs:
doi: DOI / https://doi.org/
sw: swMATH / https://swmath.org/software/
zb: zbMATH / https://zbmath.org/
wikidata: https://www.wikidata.org/wiki/